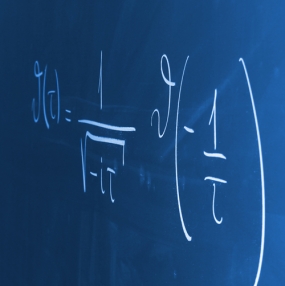
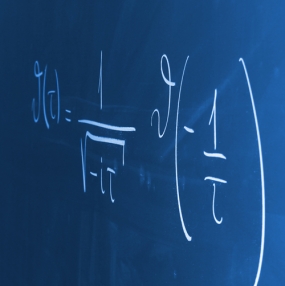
Mathematik: Arbeitsgruppe Arithmetische Geometrie
In unserer fachwissenschaftlichen Forschung befassen wir uns mit Problemstellungen der Arakelov-Geometrie und der Theorie der automorphen Formen, insbesondere der Theorie der Modulformen, sowie Fragestellungen, die an der Schnittstelle dieser beiden Gebiete liegen.
In der Arakelov-Geometrie wurde in gemeinsamen Arbeiten mit J. Burgos und U. Kühn die von C. Soulé und H. Gillet entwickelte arithmetische Schnitttheorie dahingehend verallgemeinert, dass auch hermitsche Metriken mit logarithmischen Singularitäten verwendet werden können.
Neuere Arbeiten zur Theorie der Modulformen befassen sich mit optimalen Supremumsnorm-Abschätzungen und mit Beziehungen zwischen L-Reihen zu holomorphen Modulformen und zu Maassformen.
Schließlich erwähnen wir die Arbeiten zu Abschätzungen von Arakelov-Invarianten mit Hilfe von hyperbolisch-geometrischen Methoden.
Dieser Teil der Arbeitsgruppe ist eingebunden in die Berlin Mathematical School und war bis zum Laufzeitende 31.12.2016 eingebunden in das Internationale Graduiertenkolleg Moduli and Automorphic Forms: Arithmetic and Geometric Aspects.
Leitung
Prof. Dr. Jürg Kramer
Wissenschatliche Mitarbeiter/Postdoktoranden
Ehemalige Mitglieder
- Dr. Ana María Botero
Intersection theory of b-divisors on toroidal varieties - Dr. Giovanni De Gaetano
An arithmetic Grothendieck Riemann Roch theorem for the
bundle of cusp forms on modular curves with log-singular metrics - Dr. Miguel Grados (gemeinsam betreut mit Prof. Dr. A. v. Pippich)
Arakelov intersection on modular curves
- Barbara Jung
An arithmetic analogue of Siegel’s volume formula - Antareep Mandal
Sup-norm bounds for Siegel Modular Forms - Dr. Thorsten Herrig
- Dr. Maryna Viazovska
Forschungsseminar Arithmetische Geometrie
Di, 13.00 – 15.00 Uhr, RUD 25, Raum 3.006
Arbeitsgruppe Algebraische Geometrie
Arbeitsgruppe Algebraische Zahlentheorie



