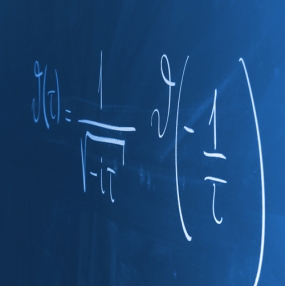
Research Group Arithmetic Geometry
Problems in Arakelov geometry and the theory of automorphic forms, in particular the theory of modular forms, are in the main focus of our
scientific research, as well problems at the interface of these two fields.
In our joint papers with J. Burgos and U. Kühn, arithmetic intersection theory as developed by C. Soulé and H. Gillet has been generalized
to also take into account hermitian metrics with logarithmic singularities.
More recent papers in the theory of modular forms deal with optimal sup-norm bounds and relations between L-series of holomorphic modular forms and Maass forms.
Last, but not least, we mention our papers on estimates of Arakelov invariants using hyperbolic geometric methods.
The members of this group are associated with the Berlin Mathematical School and till 31.12.2016 with the International Research Training Group Moduli and Automorphic Forms: Arithmetic and Geometric Aspects.
Doctoral students/Postdocs
Previous members
- Ana María Botero
Intersection theory of b-divisors on toroidal varieties - Giovanni De Gaetano
An arithmetic Grothendieck Riemann Roch theorem for the
bundle of cusp forms on modular curves with log-singular metrics - Miguel Grados (gemeinsam betreut mit Prof. Dr. A. v. Pippich)
Arakelov intersection on modular curves - Barbara Jung
An arithmetic analogue of Siegel’s volume formula - Antareep Mandal
Sup-norm bounds for Siegel Modular Forms - Dr. Thorsten Herrig
- Dr. Maryna Viazovska
Forschungsseminar Arithmetische Geometrie
Di, 13.00 – 15.00 Uhr, RUD 25, Raum 3.006
Arbeitsgruppe Algebraische Geometrie
Arbeitsgruppe Algebraische Zahlentheorie



